Computing EXP(x)

Problem Statement

The exponential function, EXP(x), is defined to be the sum of the following infinite series:

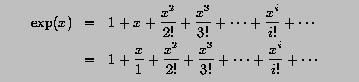
Write a program that reads in a REAL value and computes EXP() of that value using the series until the absolute value of a term is less than a tolerance value, say 0.00001.

Solution

! ---------------------------------------------------------
! This program computes exp(x) for an input x using the
! infinite series of exp(x).  This program adds the
! terms together until a term is less than a specified
! tolerance value.  Thus, two values are required:
! the value for x and a tolerance value.  In this program,
! he tolerance value is set to 0.00001 using PARAMETER.
! ---------------------------------------------------------

PROGRAM  Exponential
   IMPLICIT  NONE

   INTEGER         :: Count             ! # of terms used
   REAL            :: Term              ! a term
   REAL            :: Sum               ! the sum of series
   REAL            :: X                 ! the input x
   REAL, PARAMETER :: Tolerance = 0.00001    ! tolerance

   READ(*,*)  X                         ! read in x
   Count = 1                            ! the first term is 1 and counted
   Sum   = 1.0                          ! thus, the sum starts with 1
   Term  = X                            ! the second term is x
   DO                                   ! for each term
      IF (ABS(Term) < Tolerance)  EXIT  !    if too small, exit
      Sum   = Sum + Term                !    otherwise, add to sum
      Count = Count + 1                 !    count indicates the next term
      Term  = Term * (X / Count)        !    compute the value of next term
   END DO

   WRITE(*,*)  'After ', Count, ' iterations:'
   WRITE(*,*)  '  Exp(', X, ') = ', Sum
   WRITE(*,*)  '  From EXP()   = ', EXP(X)
   WRITE(*,*)  '  Abs(Error)   = ', ABS(Sum - EXP(X))

END PROGRAM  Exponential

Click here to download this program. 

Program Input and Output

If the input value is 10.0, the following output shows that it requires 35 iterations to reach EXP(10.0)=22026.4648. Comparing the result with the one obtained from Fortran intrinsic function EXP(), the absolute error is zero.

After 35 iterations:
  Exp(10.) = 22026.4648
  From EXP()   = 22026.4648
  Abs(Error)   = 0.E+0

If the input is -5.0, it takes 21 iterations to reach EXP(-5.0)=6.744734943E-3. The value from using Fortran intrinsic function is 6.737946998E-3 and the absolute error is 6.787944585E-6.

After 21 iterations:
  Exp(-5.) = 6.744734943E-3
  From EXP()   = 6.737946998E-3
  Abs(Error)   = 6.787944585E-6

Discussion

• One obvious way of writing this program is computing each term directly using the formula xⁱ/i!. However, this is not a wise way, since both xⁱ and i! could get very large when x or i is large. One way to overcome this problem is rewriting the term as follows:
  Therefore, the (i+1)-th term is equal to the product of the i-th term and x/(i+1). In the program, variable Term is used to save the value of the current term and is updated with
  

  Term = Term * (X / Count)
  

  where Count is the value of i+1.
• Variable Sum is used to accumulate the values of terms.
• Since the tolerance value is usually small, the first term whose value is 1 cannot be less than the tolerance value. Therefore, the computation starts with the second term and 1 is saved to Sum.
• Count indicates which term is under consideration. Its plays the role of i in the infinite series shown above.
• Since the computation starts with the first term, the value of the first term, x, is saved to Term.
• For each iteration, the absolute value of Term is checked to see if it is less than the tolerance value Tolerance. If it is, the computation is done and EXIT.
• Otherwise, this term is added to Sum and prepare for the next term. Before this, Count is increased by one to point to the next term and consequently the next term is computed as Term * (X / Count).